컴퓨터의 자료 표현법
컴퓨터는 자료를 표현하기 위해 1과0(ON & OFF, True & False)으로 이루어진 2진코드(Binary Code)를
이용하여 자료를 표현하고 저장한다.
즉, 여러분의 컴퓨터에 있는 모든 형태의 자료(숫자, 문자, 그림, 소리, 영상 등)는 컴퓨터에 2진코드로 저장되어 있다는 말이다.
위 그림은 컴퓨터에서 자주 사용되는 자료들을 정리한 자료이다. 컴퓨터에서 사용하는 자료로는
10진수, 2진수 등의 숫자를 다루는 수치자료, 영어, 한글, 특수기호등 다양한 문자를 다루는 문자자료, 참과 거짓으로 논리적인 연산을 하는 논리자료, 메모리의 위치를 이용하는 포인터자료, 여러 문자들을 이어 붙여 문장을 이루는 문자열 자료 등이 있다.
그렇다면 컴퓨터의 모든 자료를 저장하는 2진수는 어떻게 구성되어 있을까? 2진수의 기본단위인 비트(bit)는
0 또는 1하나의 숫자를 저장한다.
2진코드는 1,0 두개의 숫자 만으로 이루어져 있다. 따라서 n자리의 2진수는 2^n개의 상태를 표시할 수 있다.
또한 2진수에서 가장 앞에 있는 자릿수는 MSB(Most Significant Bit)라고 하고 가장 뒤에 있는 자릿수는 LSB(Least Significant Bit)라고 부른다.
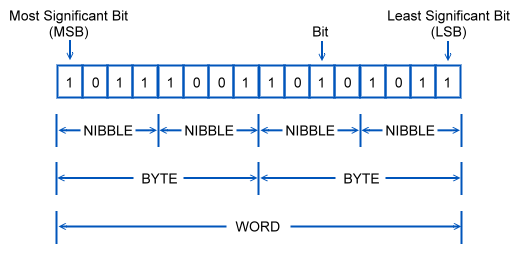
비트가 4개 모이면 니블(Nibble)이 8개가 모이면 바이트(Byte)가 된다.
4비트로 이루어진 니블(Nibble)은 16진수 1자리를 표현하기에 적합하다.
8비트로 이루어진 바이트(Byte)는 주소의 지정단위나 영문자와 숫자 한 글자의 크기이다.
10진수 표현 방식
10진수를 표현 하는 방식에는 2가지 방식이 있다.
1. 존형식(Zone Type)
10진수 한자리를 존 형식(Zone Type)으로 표현하기 위해서는 1바이트(8비트)의 공간을 필요로 한다.
이 8 비트 중 상위 4비트는 존 영역, 하위 4비트는 수치 영역으로 사용된다.
존 영역인 상위 4비트는 부호를 표시할 최하위 존 영역일 경우 1100으로 +를, 1101로 -를 표시한다. 최하위 존 영역이외의 존 영역은 1111을 사용하여 부호를 표시하지 않음을 나타낸다.
수치 영역인 하위 4 비트는 LSB(Least Significant Bit)부터 1, 2, 4, 8의 값을 가진다. 따라서 0000에서 1111까지 0-15까지 16개의 숫자를 표현 할 수 있다. 하지만 존 형식은 10진수 한자리를 나타내기 때문에 0-9까지만을 사용한다.
만약 자리가 긴 10진수를 표현하고자 한다면 표현하고자 하는 자리수 만큼 8비트 크기의 존 영역을 연결하여 사용할 수 있다.
다음 사진은 10진수 +231과 -231을 존 형식으로 나타낸 것이다.
총 24 비트를 사용하였고 이중 존 영역은 12비트를 차지하고 있다. 마지막 1의 자리의 존 영역은 1100으로 +를 1101로 -를 나타내고 있고 나머지 자릿수의 존 영역은 1111로 F값으로 채워져 부호가 아님을 나타낸다.
2. 팩형식(Pack Type)
존 형식은 10진수 한 자리 마다 4비트 크기의 존 영역을 구성해야 하기 때문에 기억공간이 낭비되고 처리가 지연된다. 이러한 문제의 해결을 위해 팩 형식(Pack Type)에서는 부호를 저장하는 최하위 존 영역을 제외한 나머지
자리의 존 영역을 제거하였다.
다음 사진은 팩 형식(Pack Type)으로 10진수 +231과 -231을 나타낸 것이다.
총 16 비트를 사용하였고 이중 존 영역은 4비트를 차지하고 있다. 마지막 1의 자리의 존 영역만을 사용하며
1100으로 +를 1101로 -를 나타내고 있다.
2 진수 표현 방식 - 정수
2진수로 정수를 표현 하는 방법은 다양하지만 가장 대표적인 3가지에 대해 알아보려고 한다.
1. 부호와 절댓값 방식(Sigh & Absolute Value Method)
위에서 서술한 내용 처럼 n비트 길이의 2진수는 2^n개의 값을 표현할 수 있다. 즉 n개 비트로는 0 ~ (2 ^ n - 1)까지의 수를 나타낼 수 있다는 말이다.
하지만 정수는 양의 정수인 자연수, 음의 정수, 0으로 이루어져 있다. 그렇기 때문에 위의 방법으로는 음수 범위를 나타낼 수 없다.
이러한 문제점을 해결하기 위해서 부호와 절댓값 표현 방식에서는 가장 왼쪽에 위치하는 최상위비트인 MSB(Most Significant Bit)를 이용하여 부호를 표시한다. 부호가 양수(+)라면 최상위 비트가 0이 되고 부호가
음수(-)라면 최상위 비트는 1이 된다. 부호를 표시하기 위해 한개의 비트를 사용하기 때문에 길이가 n비트일 경우
나타낼 수 있는 수의 범위는 -(2^ (n-1) -1) ~ (2 ^ (n-1) - 1)의 ((2 ^ n) -1)개의 수를 나타낼 수 있다.
n개의 비트를 이용하지만 나타낼 수 있는 수의 개수가 2 ^ n개가 아닌 이유는 +,- 두 부호에 대해 모두 0이
존재하기 때문이다.
즉, 부호와 절댓값 방식은 0이 +0과 -0 두 개가 동시에 존재한다는 문제가 있다.
위 사진은 부호와 절댓값 방식으로 +21과 -21을 표기한 것이다. 최상위 비트로 부호를 표시하고 나머지 비트를 이용하여 절댓값 21을 표현하였다.
2. 1의 보수 방식(1's Complement Method)
1의 보수 방식에서는 양수는 부호와 절댓값 방식과 같은 방법으로 표현하고, 음수는 2진수를
1의 보수(1's Complement)로 변환하여 표현한다. 어떤 값 -x(음수 x)를 n비트 1의 보수로 표현하는 방법은
(2 ^ n -1) - |x|이다.
위 그림은 -21을 1의 보수 형식으로 표현하는 방법을 나타낸 것이다.
전체 n 비트를 1 로 설정한값에서 x의 절댓값을 뺀 값이 x의 1의 보수가 된다.
더 간단하게 보수로 표현할 값의 절댓값에서 0은 1로 1은 0으로 바꾸어주면 1의 보수를 쉽게 나타낼 수 있다.
그림의 오른쪽을 보면 보수로 나타낼 수의 절댓값의 0을 1로 1을 0으로 바꾼 값이 그 수의 1의 보수와 같음을
알 수 있다.
3. 2의 보수 방식(2's Complement Method)
2의 보수 방식에서는 양수는 부호와 절댓값 방식과 같은 방법으로 표현하고, 음수는 2진수를
2의 보수(2's Complement)로 변환하여 표현한다. 어떤 값 -x(음수 x)를 n비트 2의 보수로 표현하는 방법은
(2 ^ n -) - |x|이다.
위 그림은 -21을 2의 보수 형식으로 표현하는 방법을 나타낸 것이다.
우선 구하려는 수의 1의 보수를 구한 뒤 1의 보수에 1을 더해주면 2의 보수가 된다.
2진수로 정수를 표현 하는 세가지 방식(부호와 절댓값 형식, 1의 보수 형식, 2의 보수 형식)을
모두 알아 보았다. 세가지 방식 모두 양수를 표현하는 방식은 모두 같다 최상위 비트를 0으로 표시한 뒤 나머지
비트를 이용하여 수를 나타낸다. 따라서 세가지 방식 모두 n개의 비트에서 0 ~ (2 ^ n-1) -1 만큼의 값을 나타낼 수 있다.
하지만 음수를 표현하는 방식은 세가지가 모두 달랐는데 최상위 비트에 1을 표시하는 부호와 절댓값 형식, n비트의 1의 보수로 표현하는 1의 보수 형식, n비트의 2의 보수로 표현하는 2의 보수 형식 세가지 모두 다른 방법으로
음수를 표시 하였다.
세가지 방식 모두 음수의 표현 범위 또한 달랐는데 부호와 절댓값 형식의 경우 최상위 비트로 부호를 표시하기
때문에 n 길이의 2진수로는 - (2 ^ n-1) ~ 0까지의 값을 표현할 수 있고 1의 보수 형식의 경우에도 - (2 ^ n-1) ~ 0까지의 값을 표현할 수 있다. 다만 두 형식 모두 -0과 +0이 공존하는 논리적 오류가 있다.
이러한 문제점을 해결한 2의 보수의 경우 음수를 - (2 ^ n) ~ -1까지 표현할 수 있다.
위 사진은 세가지 형식을 비교하여 정리한 표이다.
실수는 정수부와 소수부 사이에 소수점이 있는 숫자이다. 하지만 컴퓨터는 2진수만을 이용하여 실수를
표현해야 하기 때문에 소수점을 직접 표현하지 못하고 정수부와 실수부의 위치를 정의하여 실수를 표현한다.
2진수로 실수를 표현하는 방법에는 크게 두가지가 있다.
1. 고정소수점 형식(Fixed-Point Method)
고정 소수점 형식에서는 소수점이 항상 최상위 비트의 왼쪽 밖에 고정되어 있거나 최하위 비트의 오른쪽 밖에 고정되어 있다고 취급한다. 소수점이 항상 최상위 비트의 왼쪽 밖에 고정되어 있다고 취급하는 경우에 00010101은 0.00010101을 의미하고, 소수점이 항상 최하위 비트의 오른쪽 밖에 고정되어 있다고 취급하는 경우에 00010101은 00010101.0을 의미한다. 이런 경우에는 결국 정수표현과 같다.
2. 부동소수점 형식(Floating-Point Method)
부동 소수점 형식에서는 과학적 표기 방식(Scientific Notation)을 이용하여 실수를 표현한다.
부동 소수점 형식은 고정 소수점 표현 방식에 비해 아주 작은 값이나 큰 값을 표현할 수 있다.
예를 들어 10진수 213을 과학적 표기법으로 나타낸다면 0.213 * 10 ^ 3 이 된다.
이처럼 과학적 표기법은 지수와 가수를 이용하여 큰수와 작은수를 효율적으로 표기할 수 있는 표기법이다.
현재 컴푸터에서는 실수를 표현할때 IEEE 754 표준 표기 방식을 따르는 부동 소수점 표현 형식을 이용한다.
부동 소수점 표현 형식으로 실수를 표현하려면 부호, 지수, 가수 세영역을 사용해야 한다.
부동 소수점의 표현 범위에 따라 4바이트(32비트)의 단정도(Single Percision) 부동소수점 표현과 8바이트(64비트) 배정도(Double Percision) 부동소수점 표현으로 나뉜다.
부동소수점 표현 방식에서는 단정도의 경우 1비트의 부호비트와 8비트의 지수부, 23비트의 가수부를 가지고
배정도의 경우 1비트의 부호비트와 11비트의 지수부, 52비트의 가수부를 가지진다.

부호의 경우 정수표현 방식과 마찬가지로 0으로 양수(+)를 1로 음수(-)를 표현한다.
예를 들어 100010.101을 IEEE 754 표준에 따라 부동소수점으로 표현하면 다음의 단계를 따른다.
- 1. 정규화 : 정수부가 1이 되도록 소수점을 이동하여 과학적 표기법으로 변환한다.
100010.101 => 1.00010101 * 2 ^ 5
- 2. 부호 양수의 경우 0 음수의 경우 1을 저장한다.
예의 경우 양수이기 때문에 0을 저장한다.
- 3. 가수부 저장
정규화 과정을 거치고 나면 정수부는 항상 1이 되므로 정수부를 생략하고 소수부(00010101)만을 저장한다.
- 4. 지수부 저장
정규화 과정을 통해 구한 지수(5)와 바이어스(단정도의 경우 127, 배정도의 경우 1023)을 더한값을 저장한다.
예의 경우 단정도 방식은 5 + 127 = 132 = 10000100, 배정도 방식은 5 + 1023 = 1028 = 10000000100을 저장한다.
문자 자료 표현 방식
컴퓨터 내부에서는 문자 자료도 1과 0의 2진수 조합으로 표현한다. 문자에 대한 2진코드를 정의해 놓은 문자코드 들이 존재하는데, 대표적인 예로 BCD코드, EBCDIC코드, ASCII코드, 유니코드 등이 있다.
1. BCD(Binary-Coded Decimal)
BCD(Binary-Coded Decimal)는 6비트를 이용하며, 상위 2비트의 존 비트와(Zone Bit) 하위 4비트의 숫자 비트로 구성된다.
BCD 코드는 위 그림과 같이 존 비트(Zone Bit)와 숫자 비트를 조합하여 문자를 나타낼 수 있다.
존 비트는 00,01,10,11 등의 상태에 따라 숫자 비트가 의미하는 것이 숫자인지, 문자인지를 나타내 준다.
이러한 방법을 이용하여 0 ~ 9까지의 10진수 숫자는 물론 영어 대문자와 일부 특수문자를 나타낼 수 있다.
하지만 영어 소문자르 표시할 수 없다는 단점을 가지고 있다.
2. EBCDIC(Extended Bincary-Coded Decimal Interchange Code)
EBCDIC(Extended Bincary-Coded Decimal Interchange Code)는 미국의 IBM사가 개발한 방식로 8비트를 사용하며, 상위 4비트의 존 비트(Zone Bit)와 하위 4비트의 숫자비트로 구성되어 있다.
EBCDIC는 이름에서 알 수 있듯이 BCD를 확장하여 기존의 2비트였던 존 비트(Zone Bit)를 4비트로 늘림으로서
더 많은 문자를 표현 할 수 있게 되었다.
영어 소문자를 표현하지 못하는 BCD코드의 문제를 해결하였지만 여전히 표현 할 수 있는 문자에 한계가 있었고
영어 알파벳 이외의 다른 문자는 표현 할 수 없다는 문제점을 가지고 있다.
3. ASCII(American Standard Code for Information Interchange)
ASCII(American Standard Code for Information Interchange)는 미국 표준협의회(ASA)에서 개발한 방식으로
7비트를 이용하여며, 상위 3비트의 존 비트(Zone Bit)와 하위 4비트의 숫자 비트로 구성된다.
존비트와 숫자비트를 조합하여 0-9까지의 10진수 숫자, 영어 대소문자, 특수문자를 나타낼 수 있다.
아래의 사진은 ASCII 코드를 나타낸 코드 표이다.
코드 표에서 행은 하위 4비트의 숫자비트를, 열은 상위 3비트의 존 비트(Zone Bit)를 나타낸다.
ASCII코드는 EBCDIC코드와 같은 양의 문자를 나타낼 수 있지만 사용하는 비트의 수가 더 적어 효율적이다.
7비트의 크기를 가지기 때문에 남는 1비트를 데이터 통신 과정에서 데이터의 변조,손상을 확인할 수 있는
패리티 비트로 활용 할 수 있다는 장점 또한 가지고 있다.
하지만 ASCII또한 여전히 영어 알파벳 이외 언어의 문자를 표현 할 수 없다는 문제점을 가지고 있다.
3. 유니코드(Unicode)
BCD, EBCDIC, ASCII코드는 모두 공통적인 문제점을 가지고 있다. 바로 영어 알파벳 이외 언어의 문자를 표현 할 수 없다는 단점을 가지고 있는데 이러한 단점을 해결하기 위해 탄생한 것이 유니코드(Unicode)이다.
유니코드는 국제 표준코드(ISO/IEC 10646)로서 2바이트(16비트)의 크기를 가지고 있다.
따라서 EBCDIC, ASCII의 1바이트로 표현 할 수 없었던 다양한 언어를 표현 할 수 있게 되었다.
다양한 언어마다 정의되어 있는 유니코드표는 https://www.unicode.org/에서 확인할 수 있다.
PC(Personal Computer)가 보급되기 시작하던 때의 초기 IBM 컴퓨터 시스템에서는 BCD코드를 사용하다가
컴퓨터가 발전함에 따라 더 많은 문자를 표현할 수 있는 방안인 EBCDIC코드가 사용되었다.
그러다 미국의 표준 코드인 ASCII가 일반화 되었고, 현재는 표현의 한계를 극복하기 위해 유니코드가 일반적으로 사용되고 있다.
현재 BCD코드는 전자회로나 마이크로프로세서등의 하드웨어를 구성하는 세븐 세그먼트에 사용되고, ASCII코드는 컴퓨터 언어인 C/C++에서 문자코드로 사용되고 있다. 유니코드는 다양한 국가의 문자를 표현해야 하는 인터넷 기반 프로그램과 제품에 사용되고 있다.
기타 자료 표현 방식
컴퓨터에는 수치자료, 문자자료 이외에도 다양한 형태의 자료가 있다.
논리값을 표현하는 논리자료, 메모리의 주소를 표현하는 포인터자료, 문자를 이어붙인 문자열자료가 그 예 이다.
1. 논리 자료(Logic Data)
논리 자료는 논리값(Logic Value)를 표현하기 위한 자료 형식이다.
논리값(Logic Value)는 참(True)와 거짓(False) 중 하나를 표시한 값을 말한다.
0과 1을 이용하여 1비트로도 표현할 수 있지만 컴퓨터 내부에서는 1바이트나 1워드(Word)로 표현한다.
1바이트를 이용하여 논리자료를 표현하는 방식에는 크게 3가지가 있다.
- 1. 참은 최하위 비트를 1로 표시 하여 0000 0001로 표현하고, 거짓은 0000 0000으로 표현한다.
- 2. 참은 전체비트를 1로 표시하여 1111 1111로 표현하고, 거짓은 0000 0000으로 표현한다.
- 3. 참은 하나 이상의 비트를 1로 표시하고, 거짓은 0000 0000으로 표시한다.
2. 포인터 자료(Pointer Data)
포인터 자료(Pointer Data)는 메모리 주소를 표현하기 위한 자료 형식이다. 자료를 저장하고 있는 변수나 특정 위치의 메모리 주소를 저장하며, 주소 연산을 할때 사용한다. 포인터 자료를 사용하면 복잡한 자료구조 연산을
메모리에서의 주소 연산만으로 처리할 수 있다.
3. 문자열 자료(String Data)
문자열 자료(String Data)는 한 글자만 표현 할 수 있는 문자 자료와 달리 여러 글자로 이루어진 문자 그룹을 하나의 자료로 취급하여 메모리에 연속적으로 저장하는 자료 형식이다. 문자열 하나는 부분 문자열을 여러 개 포함할 수 있다.
부분 문자열을 포함하는 문자열 자료를 메모리에 저장하는 방법엥는 다음 세가지가 있다.
- 1. 부분 문자열 사이에 구분자를 사용하여 저장한다.
- 2. 가장 긴 문자열의 길이에 맞춰 고정길이로 저장한다.
- 3. 부분 문자열을 연속하여 저장하고 각 부분 문자열에 대한 포인터를 사용한다.
아래의 사진은 문자열 {Computer Data Struct String}을 위의 세가지 방법으로 저장한 것을 나타낸 것이다.
첫 번째 방법은 각 부분 문자열 사이에 구분자인 ;를 삽입하여 부분 문자열을 구별하였다.
이 방식의 경우 메모리 할당량이 적지만 특정 문자열을 탐색하는데 걸리는 시간이 길다.
두 번째 방법은 부분 문자열 중 가장 긴 길이를 가진 부분 문자열의 길이를 고정 길이로 활용하였다.
이 방식의 경우 가장 긴 길이의 문자열의 길이에 맞춰 공간을 할당하여 공간이 낭비되지만, 특정 문자열을 빠르게 찾을 수 있어 탐색에 걸리는 시간이 적다.
세 번째 방법은 문자열의 각 문자에 해당하는 메모리 주소를 이용하는 방식이다.
이 방식의 경우 메모리 할당량이 가장 작고 특정 문자나 부분 문자열을 찾을 때에도 메모리 연산을 이용하여
굉장히 효율적으로 탐색할 수 있어 탐색에 걸리는 시간 또한 적다.
'자료구조, 알고리즘' 카테고리의 다른 글
| DS04 - 포인터 (0) | 2018.05.13 |
|---|---|
| DS03 - 배열(Array) (0) | 2018.05.12 |
| AL02 - 알고리즘의 성능 분석 (0) | 2018.05.07 |
| AL01 - 알고리즘의 이해 (0) | 2018.05.07 |
| DS01 - 자료구조의 정의와 분류 (0) | 2018.04.28 |














