본 게시물은 University of Arizona의 Prof. J. Scott Tyo의 OPTI512R 강의를 보고 정리한 내용입니다.
전공자가 아닌 만큼 부정확한 정보가 포함되어 있을 수 있습니다.
부정확한 정보가 있다면 알려주시면 감사하겠습니다.
Definition of Convolution
앞선 Lec 4에서 Input $f(x)$와 Impulse Response $h(x)$의 관점에서 output $g(x)$를 다음과 같이 쓸 수 있게 해 주는 LSI System의 속성에 대해 학습하였다.
$$g(x) = \int^{\infty}_{-\infty} f(\alpha)h(x-\alpha) d\alpha$$
위 수식의 Integral은 Convolution integral로 알려진 special integral으로, Convolution의 Mathematical, Notational 한 representation은 다음과 같다.
$$f(x) * h(x) = \int^{\infty}_{-\infty} f(\alpha)h(x-\alpha) d\alpha$$
아래 그림은 Linear System의 Schematic을 나타낸 것이다.

Graphical Convolution
Convolution integral은 항상 direct integral을 통해 계산 될 수 있고, 많은 종류의 function에 있어 direct integration이 가능하지만, Graphical method를 활용하는 것이 더 쉬울 때가 많다. 또한 Graphcial method는 현재 진행 중인 convoltuion process에 대한 physical 하게 이해하는데 도움이 된다.
$$f(x) = rect({{x-1} \over 2}) \\ h(x) = ramp(x)rect({{x-1.5} \over 3})$$
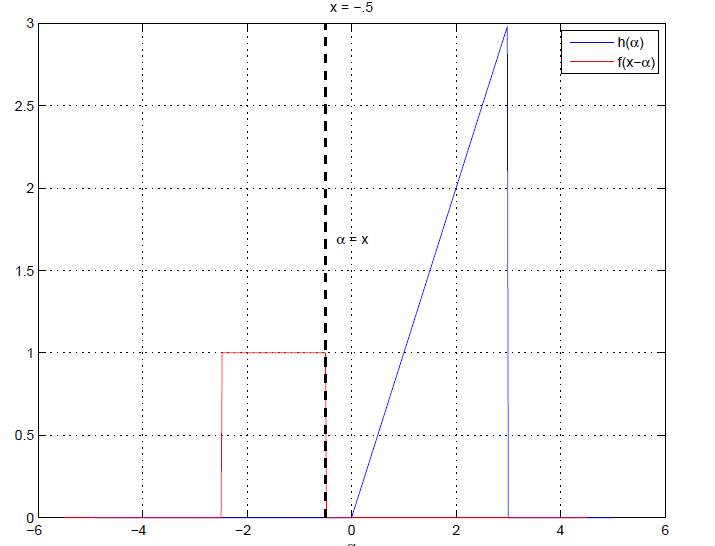
위와 같은 두 function이 있다고 할 때, 아래의 그림은 서로 다른 3개의 $x$ value에 대한 f(x-\alpha)$와 $h(\alpha)$를 나타낸 것이다.

$x < 0$ 일 때는 두 function의 graph가 overlap되지 않고, $0 \leq x \leq 5$의 구간에서는 partial 하게 overlap 되고 있다. $x > 5$인 구간부터는 다시 두 function의 graph가 overlap 된 면적이 0이 된다. 아래 그림과 같이 $x=3$인 rectangular pulse가 완전히 half-triangle에 있을 때, maximal overlap이 발생한다.

위의 자료들을 참고하여 Graphic convolution을 수행하는 방법을 아래와 같이 설명할 수 있다.
1. 먼저 두 signal을 가져와 $\alpha$의 function으로 plot한다.
2. 두 signal 중 하나를 flip 하고, $-\alpha$의 function으로 만든다.
3. 해당 singal을 $x$만큼 offset 한다.
5. 이동되고 뒤집힌 function에 이동되지 않은 function을 곱하고, $\alpha$에 대해 integral 한다.
이 integral의 결과는 한 위치에서 $g(x)$를 제공한다. 관심 있는 $x$의 모든 value에 대해 이 process를 반복하여 LSI System의 output을 얻을 수 있다.
Direct Evaluation of the Convoution Integral
Graphic Convolution을 사용할 때 발생하는 문제점은 두 Function 간의 overlap Area를 파악하고 해당 Area를 integral 해야 하지만, 때로는 이 연산이 상당히 까다로울 수 있다는 점이다. 예를 들기 위해 두 function을 다음과 같이 정의하였다.
$$f(x) = rect({{x-1} \over 2}) \\ h(x) = ramp(x) rect({{x-1.5} \over 3})$$
$g(x) = f(x) * h(x)$를 계산하기 위해 우리는 다음과 같은 integral을 사용해야 한다.
$$g(x) = \int^{\infty}_{-\infty} h(\alpha)f(x-\alpha) d\alpha$$
$h(\alpha)$는 $0 \leq \alpha \leq 3$의 구간에서만 0이 아닌 값을 가지고, $f(\alpha)$는 $x-2 \leq \alpha \leq x$의 구간에서 0이 아닌 값을 가진다. 이는 곧 위의 두 구간의 intersection에서만 0이 아닌 곲을 가진다는 의미이다.
1. $x < 0$ 일 때, 두 구간은 overlap 되지 않기 때문에,$x <0$에 대해 $g(x) = 0$이다.
2. $0 \leq x \leq 2$의 구간에서, lower limit는 $\alpha = 0$으로 설정되고, upper limit는 $\alpha = x$로 설정된다.
이때 $g(x) = \int^x_0 \alpha d\alpha = {x^2 \over 2}$이다.

3. $x$가 2 보다 커지면, lower limit은 input에 의해 설정되고, $2 \leq x \leq 3$의 구간에서 $g(x) = \int^{x}_{x-2} \alpha d\alpha = {\alpha^2 \over 2} |^2_{x-2} = 2(x-1)$이다.

4. $x=3$에서 upper limit은 $h(x)$에 의해 제한되고, $3 \leq x \leq 5$의 구간에서 $g(x) = \int^{3}_{x-2} \alpha d\alpha = {\alpha^2 \over 2} |^3_{x-2} = {5\over 2} - {x^2 \over 2} + 2x$이다.

5. $x = 5$일 때, 다시 한번 두 function 간의 overlap area의 면적이 0 가 되고, convolution 은 0 이 된다.

이 모든 결과를 정리하면 다음과 같다.
$$ f(x) * g(x) = \begin{cases}0 & x \leq 0\\{x^2 \over 2} & 0 \leq x \leq 2 \\ 2(x-1) & 2 \leq x \leq 3 \\ {5\over2}-{x^2 \over 2} + 2x & 3 \leq x \leq 5 \\ 0 & x > 5\end{cases} $$
Properties of Convolution
Convolution operator에는 Convolution integral을 조작할 수 있는 여러 가지 중요한 property가 존재한다.
1. Commutative Property
아래와 같은 Convolution이 정의되어 있을 때.
$$f(x) * h(x) = \int^\infty_{-\infty} f(\alpha)h(x-\alpha) d\alpha$$
$\beta = x - \alpha$, $d\beta = -d\alpha$로 variable을 변경하였을 때 아래와 같은 관계가 성립한다.
$$f(x) * h(x) = \int^\infty_{-\infty} f(x-\beta)h(\beta) d\beta \\ f(x)*h(x) = h(x) * f(x)$$
이는 우리가 편의에 따라 Convolution의 순서를 결정할 수 있다는 것을 알게 한다는 점에서 매우 중요하다.
2. Distributive Property
Convolution Operator가 Linear 함에 따라, 다음의 관계가 성립한다는 것이 자명하다.
$$f(x)*\left[ah_1(x) + bh_2(x)\right] = af(x) * h_1(x) + bf(x)*h_2(x)$$
3. Shift Invariance
Convolution의 Function 중 하나가 Shift 되는 것에 대해 고려해보자. 아래와 같은 식이 있다고 할 때
$$f(x) * h(x) = g(x)$$
다음의 관계 가 성립한다.
$$f(x-x_0) * h(x) = \int^\infty_{-\infty} f(\alpha-x_0)h(x-\alpha) d\alpha \\ = \int^\infty_{-\infty} f(\beta)h(x-x_0-\beta) d\beta \\ = g(x-x_0)$$
이는 Convolution 이 Shift Invariance 하다는 것을 의미한다.
4. Associative Property

위 그림과 같은 System이 존재한다고 할 때, 이 System은 System 1의 Output이 System 2의 Input으로 공급되고, 최종 ouput이 다음과 같은 cascaded System이다.
$$\left[f(x) * h_1(x)\right]*h_2(x) = \int^\infty_{-\infty}\int^\infty_{-\infty} f(\alpha)h_1(\beta-\alpha)d\alpha\;h_2(x-\beta)d\beta \\ = \int^\infty_{-\infty}f(\alpha)\int^\infty_{-\infty}h_1(\beta-\alpha)h_2(x-\beta)d\beta d\alpha \\ = \int^\infty_{-\infty}f(\alpha)\left[h_2(x)*h_1(x-\alpha)\right]d\alpha \\ = \int^\infty_{-\infty} f(\alpha)g(x-\alpha)d\alpha \\ = f(x)*\left[h_2(x)*h_1(x)\right]$$
위 식에서 우리는 $g(x) = h_1(x) * h_2(x)$를 정의하였다. 이는 System의 실제 순서와 상관없이 input, output 및 impulse response를 grouping 할 수 있다는 것을 의미한다.
Convolution With $\delta$-Functions and Comb Function
1. $\delta$-Functions
이전에 우리는 $\delta$-function이 아래와 같은 property를 가지고 있다는 것을 확인하였다.
$$f(x) * \delta(x-x_0) = \int^{\infty}_{-\infty} f(\alpha)\delta(x-x_0-\alpha)d\alpha \\ = f(x-x_0)$$
마찬가지로 우리는 $delta$-function의 derivative에 대해서 다음과 같이 convoltuion 할 수 있다.
$$f(x) * \delta^{(k)}(x-x_0) = \int^{\infty}_{-\infty} f(\alpha) \delta^{(k)}(x-x_0-\alpha) \\ = f^{(k)}(x-x_0)$$
$\delta$-function의 derivative argument가 $(\alpha -x)$가 아니라 $(x - \alpha)$이기 때문에, 위 수식에는 $(-1)^k$ 항이 없다.
2. Comb Function
Comb Function으로 Convolution을 확장할 수 있다.
$$f(x) * comb(x) = f(x) * \sum^\infty_{n=-\infty} \delta(x-n) \\ = \sum^\infty_{n=-\infty} f(x)*\delta(x-n) \\ = \sum^\infty_{-\infty} f(x-n)$$
위 식에서 우리는 convolution이 input function $f(x)$의 copy를 생성하지만, 각 copy는 argument의 integer value로 offset 된다는 점을 확인할 수 있다.
아래 수식과 같은 convolution을 정의되어 있고, 그 결과는 아래 그림과 같다.
$$tri(x) * {1 \over 2} comb({x \over 2}) = \sum tri(x-2n)$$

만약 임의의 function $f(x)$가 있고, 헤다 function에 convolution을 적용한다면, 그 결과는 $T$의 Period를 가지는 Periodic function이다. $|x| > {2\over T}$일 때, $f_p(x) = 0$이고, 하나의 period가 $f_p(x)$에 의해 설명된다.
$$f_p(x) = f(x) * {1\over T} comb({x \over T})$$
Correlation
Correlation은 Physics의 많은 측면에서 자주 나타나는 매우 중요한 operation이다. Correlation은 두 Function 간의 Similarity를 측정하는 것으로 다음과 같이 정의된다.
$$\gamma_{fg}(x) = \int^\infty_{-\infty} f(\alpha) g^*(\alpha-x) d\alpha$$
위 수식을 살펴보면 Correlation이 Convolution의 수식과 상당히 유사하지만 Function 중 하나의 Argument가 Flip 되어 있다는 사실을 확인할 수 있다. Correlation의 Complex Conjugate는 다음과 같이 정의된다.
$$\gamma_{gf}(x) = \int^\infty_{-\infty} g(\alpha) f^*(\alpha-x) d\alpha \\ = \int^\infty_{-\infty} f^*(\beta) g(\beta + x) d\beta \\ = \gamma^*_{fg}(-x)$$
이때 $g(x) = f(x)$가 성립하는 speical case를 Autocorrelation Function이라고 하고, 이를 수식으로 표현하면 아래와 같.
$$\gamma_f(x) = \int^\infty_{-\infty} f(\alpha) f^*(\alpha-x) d\alpha$$
Correlation의 Symmetry propery는 $\gamma(x) = \gamma^*_f(-x)$를 의미하며, 이는 Correlation이 Hermitian function임을 의미한다.(${d^2y \over dx^2} - 2x {dy \over dx} + 2ny = 0$의 Hermitian differential equation을 만족하는 Function)
또한 Correlation은 Schwarz inequality를 상용하여 증명할 수 있는 다음과 같은 Property를 가진다.
$$|\gamma_f(x)| \leq |\gamma_f(0)|$$
또한 Correlation과 Convolution은 다음과 같은 차이점들을 가지고 있다.
1. Correlation Integral에서 2번째 function은 complex conjugate를 가지지만, Convolution의 경우 두 function 모두 Conjugate를 가지지 않는다.
이는 곧 Correlation의 경우 어떠한 Function에 Correlation을 적용할 경우 Conjugate를 통해 Inverse operation을 수행하여 original input function을 복원해 낼 수 있지만, Convolution의 경우에는 Conjugate가 존재하지 않기 때문에 inverse operation을 구할 수 없어 Original Input Function을 복원할 수 없다는 것을 의미한다.
2. Correlation의 Shifted Function에는 Argument $(\alpha - x)$가 있지만, Convolution의 Shifted function에는 argument $(x-\alpha)$가 있다.(둘 다 $\alpha$에 대해 integral 한다.) 앞서 우리는 Convoltuion에서 $(x - \alpha)$를 취하는 것의 효과가 두 function 중 하나를 flip 하는 것이라고 학습하였다.
위 두 가지 사실에 비추어 다음과 같이 정의할 수 있다.
$$\gamma_{fg}(x) = f(x) * g^*(-x)$$
'Optics > 이론' 카테고리의 다른 글
| Lec 7. Special Properties and Important Theorems Involving the Fourier Transform (0) | 2021.08.03 |
|---|---|
| Lec 6. The Fourier Transform and its Properties (1) | 2021.07.29 |
| Lec 4. Operators and Linear, Shift-Invariant Systems (0) | 2021.07.21 |
| Lec 3. Harmonic Analysis and the Fourier Series (0) | 2021.07.06 |
| Lec 2. Special Function (0) | 2021.06.29 |