본 게시물은 University of Arizona의 Prof. J. Scott Tyo의 OPTI512R 강의를 보고 정리한 내용입니다.
전공자가 아닌 만큼 부정확한 정보가 포함되어 있을 수 있습니다.
부정확한 정보가 있다면 알려주시면 감사하겠습니다.
Ideal Sampling
지금 까지 우리는 모든 function을 Continuous function으로 간주하였다. 즉 function $f(x)$는 우리가 선택한 임의의 $x$에 대해 항상 value를 가졌다. 자연에서 발생되는 Analog signal의 경우 Countinuous 하지만, Computer를 비롯한 digital device는 Discrete 한 Digital signal을 사용한다. Digital device에서 Analog signal을 처리하고 사용하기 위해 Countinuous 한 signal을 sampling 하거나, discrete function으로 표현해야 한다. 본 Lecture에서는 finite sample collection에서만 uderlying continuous function을 ideally reconstruction 할 수 있는 상황만을 다룰 것이다.

위 그림과 같은 Bandlimit function $f(x)$를 고려해보자. Band limit를 적용함으로써 우리는 Signal의 Spectrum이 특정 range를 벗어나면 0이 되도록 할 수 있고, 이는 수학적으로 다음과 같다.
$$F(\xi) = 0 ,|\xi| > {W \over 2}$$
Band limit이 적용된 signal는 다음과 같은 feature를 가지고 있다. Spectrum이 finite support를 가지기 때문에, Signal $f(x)$는 반드시 Infinite support를 가져야 한다. 즉, signal은 절대로 0이 되지 않는다. 이는 Heisenberg uncertainty relationship의 결과이다. 또한 signal에 존재하는 High frequency에 limit가 있기 때문에. signal에 허용되는 minimum smoothness로의 transition speed에 limit이 있다. Whittaker-Shannon Sampling theorem은 Band limit이 적용된 signal이 W 이상의 speed로 sampling 될 경우 정확하게 Reconstruction 될 수 있음을 알려준다.
(강의에서는 Whittaker-Shannon Sampling Theorem이라고 소개를 하였지만, 본래 Nyquist-Shannon Sampling Theorem으로 알고 있던 Theorem이라 찾아보니, 이전에 Whittaker에 의해서도 별견되었고, Shannon이 Whittaker의 논문을 cite 하여 Nyquist-Shannon 외에도 Whittaker-Shannon, Whittaker-Nyquist-Shannon 등의 아명으로 불리고 있다고 한다.)
Ideally Sampled Signal을 생성하기 위해 Band limit function에 comb function을 multiply 한다.
$$f_s(x) = f(x) {1 \over x_s} comb({x \over x_s}) \\ = sum_n f(nx_s)\delta(x-nx_s)$$
이때 $x_s$는 Sampling interval이고, $\xi_s = {1 \over x_s}$는 Sampling frequency이다. 이 Process는 아래 그림에서 확인할 수 있다.

Sampled signal의 Spectrum은 Convolution theorem을 활용하여 다음과 같이 정의할 수 있다.
$$F_s(\xi) = \mathcal{F} \{f_s(x)\} = F(\xi) * comb(x_s \xi) \\ = {1 \over x_s} \sum_n F(\xi -n \xi_s) \\ =\xi_s \sum_n F(\xi-n\xi_s)$$
위 수식을 통해 우리는 Sampled signal이 periodic 하며 아래 그림과 같이 Unsampled signal의 spectrum에 대해 무수히 많은 copy를 가지고 있음을 알려준다.
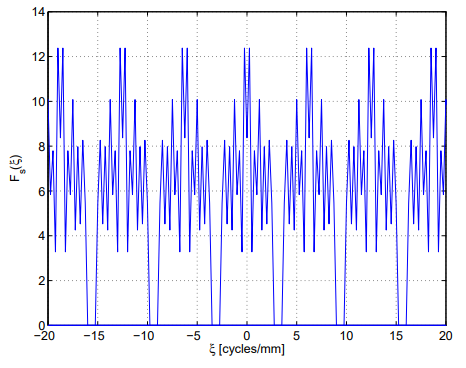
위 그림에서 우리는 Sampling Frequency $\xi_s$가 W보다 클 때, Signal Spectrum의 copy가 overlap 되지 않는다는 것을 확인할 수 있다. 이 Minimum sampling frequency를 Nyquist Sampling Frequency라고 한다. Ideal sampling과 Band-limited reconstruction의 전체 process는 아래 그림에 나와 있다.

Reconstruction
위의 reconstruction process는 우리가 Ideal 하게 Reconstruction을 할 수 있다는 것을 알려주지만, 이는 오로지 Frequency domain에 국한되어있다. 이제 Space domain에서의 reconstruction process에 대해 알아보도록 하자.
Ideal reconstruction을 제공하는 low pass filter는 다음과 같이 정의된다.
$$H(\xi) = rect({\xi \over W})$$
이 Filter는 다음과 같은 impulse response를 가진다.
$$h(x) = W sinc(Wx)$$
Filter의 output인 reconstructed signal은 다음과 같다.
$$g(x) = f_s(x)*h(x) \\ = [\sum_n f(nx_s)\delta(x-nx_s)] * W sinc(Wx) \\ = W\sum_n f(nx_s)sinc(W(x-nx_s))$$
위 수식은 Band limited signal이 weighted, shifted sinc function의 superposition으로 작성될 수 있음을 알려준다.
Aliasing
만약 Sampling rate가 너무 낮아 $\xi_s < W$가 되면, 어떤 일이 일어날 것 같은가? 이 경우 Spectrum $F(\xi)$의 copy들이 overlap 되어 아래 그림과 같이 information을 제대로 reconstruction 할 수 없다. 특히 High frequnecy에 담긴 informatino이 Low frequnecy로 Aliasing 된다. 이러한 현상을 Aliasing이라고 하며, 이는 Sampling interval이 Nyquist Frequency보다 작을 때 발생하게 된다.

위 그림의 오른쪽 그림을 보면, Nyquist frequnecy에 해당하는 한 period당 2개씩 sampling을 수행하는 것이 아닌, period당 1개씩 Sampling을 수행하고 있다는 사실을 Sapce domain에서 확인할 수 있다. Aliasing의 대표적인 예는 다음 동영상에 나타나 있다. 동영상의 30초 분 경부터 Propeller의 회전수가 촬영 장치의 최대 주파수를 넘게 되면서 Propeller의 회전 방향이 반대로 도는 것처럼 보이고, 형태가 뒤틀려 보이게 된다.
Sampling And Periodicity
우리는 Fourier Transform을 Fourier Integral의 측면에서 다음과 같이 정의하였다.
$$F(\xi) = \int^\infty_{-\infty} f(x) e^{-j2\pi \xi x} dx$$
Ideally sampled function의 Fourier Transform은 다음과 같다.
$$F_s(\xi) = \int^\infty_{-\infty} \sum^\infty_{k=-\infty} f(k\triangle x)\delta(x-k \triangle x) e^{-j2\pi \xi x} dx \\ = \sum^\infty_{k=-\infty}f(k \triangle x)e^{-j2\pi \xi k \triangle x} = \sum^\infty_{k=-\infty}f_k e^{-j2\pi \xi x \triangle x}$$
이 Series는 다음과 같은 Property를 가진다.
1. Series내의 많은 sample이 0일지라도 이것은 명백히 Infinite series이다.(위 수식의 마지막 항은 Lecture 4에서 다룬 Periodic function에 대한 Fourier Series representation과 상당히 유사하다.)
2. Function $F(\xi)$는 Frequency variable $\xi$에서 Continuous 하다.
3. Function $F(\xi)$는 Frequency variable $\xi$에서 Periodic 하다.
이러한 Transform에는 많은 이름이 있는데, function $f(t)$가 time에 따라 달라지는 Communication system에서는 Discrete Time Fourier Transform이라고 한다. 우리는 일관성을 위해, 이 Transform을 Discrete space Fourier Transform이라고 부르도록 하겠다.
'Optics > 이론' 카테고리의 다른 글
| Lec 14. Discrete Convolution (0) | 2021.08.16 |
|---|---|
| Lec 13. Discrete Fourier Transform (0) | 2021.08.16 |
| Lec 11. Signal Processing (0) | 2021.08.13 |
| Lec 10. Filters (1) | 2021.08.13 |
| Lec 9. Hankel Transform, Fourier Bessel Transform, and Radon Transform (2) | 2021.08.12 |