본 게시물은 University of Arizona의 Prof. J. Scott Tyo의 OPTI512R 강의를 보고 정리한 내용입니다.
전공자가 아닌 만큼 부정확한 정보가 포함되어 있을 수 있습니다.
부정확한 정보가 있다면 알려주시면 감사하겠습니다.
Extraction of Signal From Additive Noise
원하는 signal $s(x)$와 noise process $n(x)$로 구성된 다음과 같은 signal $f(x)$가 있다고 하자.
$$f(x) = s(x) + n(x)$$
이를 Additive noise model이라고 하며, Noise가 Signal과 Independent 하다고 가정하였다. 우리의 목표는 아래 그림과 같이 Noise를 걸러낼 수 있는 LSI System을 개발하여 Signal을 최대한 충실하게 보존하는 것이다. Convolution의 Additive property로 인하여, Transfer function은 Signal과 Noise 모두에 대해 작동하며 System의 output은 다음과 같다.
$$g(x) = [s(x) + n(x)] * h(x)$$

아래 그림은 Gaussian Signal에 일부 noise가 추가된 예시이다. 만약 우리가 $S(\xi)$와 $N(\xi)$에 대한 사전 지식이 있다면 우리는 다음과 같이 Filter를 정의할 수 있다.
$$H(\xi) = {S(\xi) \over {S(\xi) + N(\xi)}}$$

System의 Output은 다음과 같다.
$$G(\xi) = (S(\xi) + N(\xi)) {S(\xi) \over S(\xi) + N(\xi)} = S(\xi)$$
이를 위한 Filter는 아래 그림과 같다.
물론 이는 극히 비현실적인 예시로, 현실에서는 Noise가 Random 하기 때문에, Noise의 Spectrum을 정확하게 알 수 없다. 게다가 우리가 위 수식에서 가정한 것과 같이 $S(\xi)$를 알고 있다면, $s(x)$를 알 수 있었을 것이기 때문에, 이를 측정할 필요가 없었을 것이다. 아래 그림은 위 그림의 filter를 동일한 statistic을 가지는 다른 noise가 추가된 signal의 모습을 나타낸 것이다. 그림에서 알 수 있듯이, Reconstruction이 완벽하지 않다는 것을 확인할 수 있다.

우리는 $H$를 다음과 같이 정의하여 filter의 특성을 검사할 수 있다.
$$H(\xi) = {S(\xi)/N(\xi) \over {S(\xi)/N(\xi)+1}}$$
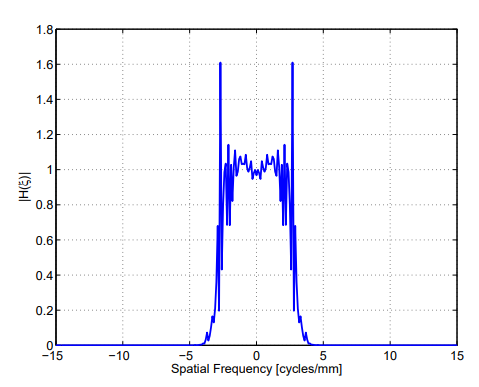
Frequency range가 $|S(\xi)| >> |N(\xi)|$인 경우(SNR이 높을 경우), Filter는 $H \rightarrow 1$에 approach 하고, $|S(\xi)| << |N(\xi)|$인 경우 $H \rightarrow 1$에 approach 한다. 우리는 이것을 Filter를 설계하는데 이용할 수 있다. 간단하게 Signal + Noise에서 SNR이 높고 다른 곳에서는 0인 Ideal BPF를 곱하기만 하면 된다. 이 예제의 경우, filter는 $\xi = 0$을 중심으로 $5[cycles/mm]$의 Rectangular window가 된다. 이 filter의 결과는 아래 그림과 같다.
Equalization
거의 모든 Realistic scenario에서, data를 기록하는 measurement system은 측정할 signal에 약간의 perturbation을 일으킨다. 이는 Linear system으로 modeling 될 수 있으며, System에 대한 Input은 측정할 알려지지 않은 signal $f(x)$이고, output information(기록)은 $f(x) * h(x)$이다. 원칙적으로 Impulse Response $h(x)$는 calibration을 통해 결정될 수 있다. Impulse Response의 Effect를 제거할 수 있을까? Audio system에 사용되는 Graphic Equalizer가 이러한 역할을 하는 대표적인 system의 예이다.

위 그림에 표시된 것과 같은 signal은 다음과 같이 정의된다.
$$s(x) = rect({x-4 \over 2})\cos(4\pi x)$$
이 Signal은 다음과 같은 Gaussian LPF transfer function을 가지고 있는 System에 의해 측정된다.
$$H(\xi) = Gaus({\xi \over 5})$$
Output에서는 위 그림에 볼 수 있듯이 LPF의 특징인 Sharp edge와 overall amplitude, energe의 reduction을 관측할 수 있다.
일반적으로 우리는 System의 Output이 Input $f(x)$에 filter $H(\xi)$를 Convolution 한 결과이기 때문에, Deconvolution filter $1 \over H(\xi)$를 multiply 하여 filter의 effect가 제거될 것이라고 생각할 수 있다. 하지만 단순히 이 예제에서만 하더라도 $|H(\xi)| << 1$이 성립하는 $\xi$의 값이 많기 때문에, Inverse filter가 나쁜 영향을 미치게 된다. 아래 그림과 같은 예를 통해 자세히 알아보자. 우리는 signal에 극 소량의 noise($SNR = 2 x 10^5$)를 추가하였다. 그러나 이 극소량의 nosie는 High frequency에서 Inverse filter에 의해 Amplify 된다.

만약 우리가 Equalization filter의 band를 $-5 < \xi < 5$로 제한한다면, 보다 합리적인(여전히 약간의 문제가 있지만) reconstruction을 얻을 수 있다. 좋은 Equalization 결과를 얻기 위해서는 Equalization filter의 stability와 측정의 SNR을 이해하고, 이를 이용할 줄 알아야 한다.
Matched Filter
Matched filter는 특정 signal이 존재하는지를 알리도록 설계된 correlation-based construction이다. matched filter는 원래 radar signal processing을 위해 설게 되었으나, noise와 interference의 영향을 받은 signal에서 관심 있는 signal을 찾기 위한 detection 및 estimation에 널리 사용되게 되었다.
Matched filter는 주어진 signal에서 우리는 원하지 않는 signal $\{n_i(x)\} = \{n_1(x), n_2(x), ....\}$을 detecting하지 않으면서, 주어진 signal에 존재할 수도 있고 존재하지 않을 수도 있는 관심 있는 signal $s(x)$를 detecting 하는 것을 수행한다. 이를 수학적으로 나타내면(편의를 위해 signal을 normalize 하였음) 다음과 같다.
$$\int^\infty_{-\infty} |s(x)|^2 dx = \int^\infty_{-\infty} |n_i(x)|^2 dx = k$$
우리가 LSI System을 가지고 있다고 가정해보자. System에 signal이 지속적으로 들어오고 있을 때, 이 signal은 우리가 원하는 $s(x)$일 수도 있고, noise 혹은 interference일 수도 있다. 가령 Filter의 impulse response인 $h(x) = s^*(-x)$가 우리가 detect 하고자 하는 signal의 time-reversed, complex conjugate라고 하면, 이 경우 우리는 다음을 얻을 수 있다.
$$g(x) = f(x) * s^*(-x)$$
$f(x) = s(x)$이면, 원하는 signal의 correlation function이라고 하는 $g(x) = \gamma_s(x)$가 된다. Autocorrelation function의 property로 인해 $g(x)$가 x=0에서 maximum이 되며, $g(x) \leq g(0)$임을 알 수 있다. $f(x) = n_i(x)$ 일 때는 다음이 성립하게 된다.
$$g(x) = \gamma_{n_is}$$
Output의 Amplitude를 고려해보자.
$$|\gamma_{{n_i}s}| = |\int^\infty_{-\infty} n_i(\alpha)s^*(\alpha -x)d\alpha| \\ \leq [\int^\infty_{-\infty} |n_i(\alpha)|^2 d\alpha]^{1\over2}[\int^\infty_{-\infty} |s(\alpha)|^2 d\alpha]^{1\over2} \\ \leq k = \gamma_s(0)$$
이러한 Inequality를 Shwarz inequality라고 하며, interfering signal의 output이 항상 input이 원하는 signal일 때의 output보다 작거나 같음을 알려준다. interfering signal이 single Gaussian noise process의 realization인 경우 matched filtering이 최적의 방법이라는 것이 잘 알려져 있다.
Interference를 suppress 하는데 도움이 될 수 있는 matched filtering process를 추가로 modify 할 수 있지만, 이러한 filtering이 non-Gaussian일 경우, matched filtering을 능가하는 tool을 개발할 수 있다.
1. Optical Character Recognition(OCR)
matched filter의 application 중 하나는 Optical Character Recognition(OCR)이다. 초창기에 OCR은 실제로 Lens의 Foureir Transform property를 사용하였으나 현재는 Electronic method를 사용한다. 아래 그림은 우리가 구별하고자 하는 4개의 character이다.

아래 그림은 위의 4가지 경우 각각에 대해 character "C"에 해당하는 filter를 convolution 한 결과이다.
이는 matched filtering process를 이해하는 데 큰 도움이 된다. 왼쪽 아래의 그림의 output이 가장 큰 value와 좁은 peak를 가진다. 이는 왼쪽 하단의 input("C")이 우리가 찾고 있는 signal임을 의미한다. 그러나 오른쪽의 두 그림은 상대적으로 높은 correlation을 생성하고 있는데, 위 그림의 character를 검토하여 원인을 알 수 있다. character "C"는 형태적으로 "C"와 가장 correlation이 높지만, "B"와"D"와도 상당한 correlation이 있다. 반면 "A"와는 형태적으로 낮은 Correlation을 가지고 있으며, 이는 Filter의 출력에 반영된다.

'Optics > 이론' 카테고리의 다른 글
| Lec 13. Discrete Fourier Transform (0) | 2021.08.16 |
|---|---|
| Lec 12. Sampling & Reconstruction (2) | 2021.08.14 |
| Lec 10. Filters (1) | 2021.08.13 |
| Lec 9. Hankel Transform, Fourier Bessel Transform, and Radon Transform (2) | 2021.08.12 |
| Lec 8. Two Dimensional Functions, Convolution, and Fourier Transforms (0) | 2021.08.11 |