본 게시물은 University of Arizona의 Prof. J. Scott Tyo의 OPTI512R 강의를 보고 정리한 내용입니다.
전공자가 아닌 만큼 부정확한 정보가 포함되어 있을 수 있습니다.
부정확한 정보가 있다면 알려주시면 감사하겠습니다.

위와 같은 System이 있을 때, Frequency domain에서 system을 고려해보면, Transform fucntion이 자신의 Fourier Transform $F(\xi)$에 의해 input signal의 Frequency를 modify 한다고 생각할 수 있다. 이처럼 Input의 Spectral property를 filtering 하여 원하는 output을 생성하는 역할을 하는 장치를 Linear Filter라고 한다.
Transfer function의 magnitude와 phase를 다음과 같이 정의할 수 있다.
$$H(\xi) = A_H(\xi)e^{-j\phi_H(\xi)}$$
$A_H(\xi)$는 filter의 Amplitude sepctrum, $\phi_H(\xi)$는 phase spectrum이며, Amplitude와 Phase spectra는 서로 다르다.
The 4-F Imaging System
앞으로 우리는 Fourier Optics의 구성 요소인 Diffraction과 Imaging의 principle에 대해 학습할 것이다. 학습에 앞서 우리는 Imaging context에서 filtering property를 다룰 수 있는 System을 정의할 것이다.
아래 그림과 같이 Lens의 focal length $f$와 $\lambda$의 wavelength를 가지는 Geometry가 있다고 가정할 때, Lens의 back focal plane($u_2$)에 있는 field를 front focal plane($u_1$)에 있는 field로 다음과 같이 쓸 수 있다.

$$u_2(x_2, y_2) \propto \int\int^\infty_{-\infty} u_1(x_1, y_1) e^{-j{2\pi \over \lambda f}(x_1x_2+y_1y_2)}dx_1dy_1$$
위 수식에서 다음의 변환을 적용하면,
$$\xi = {x_2 \over \lambda f} \\ \eta = {y_2 \over \lambda f}$$
아래와 같은 결과를 얻게 된다.
$$u_2(x_2, y_2) \propto \int \int^\infty_{-\infty} u_1(x_1, y_1) e^{-j2\pi(x_1 \xi + y_1 \eta)}dx_1 dy_1$$
위 수식이 Two-Dimensional Fourier Transform이라는 것은 쉽게 인지 할 수 있으며, 이는 Lens의 Back focal plane field 가 Lens의 Front focal plane field에 비례한다는 관계가 존재한다는 매우 중요한 관계이다. $x_1$이 length의 unit을 가지기 때문에 $\xi$는 반드시 Inverse length의 unit을 가져야 한다는 것을 알 수 있고, 실제로 $\xi = {x_2 \ over (\lambda f)}$는 이러한 unit을 가진다.
이제 우리는 Lens의 Fourier Transform Property를 알게 되었기 때문에, 두 개의 lens를 사용하여 아래 그림과 같은 4-f imaging system을 구축할 수 있다. -1의 magnification을 가지는 이 System을 이용하여 ray tracing을 수행할 수 있으며, 이는 Image Relay system처럼 동작한다.

첫 번째 Lens는 위 수식과 같이 Fourier Transform을 수행한다. 두 번째 Lens의 Back focal plane fields를 결정하는 유사한 과정을 아래와 같이 정의할 수 있다.
$$u_3(x_3, y_3) \propto \int \int^\infty_{-\infty} u_2(x_2, x_2) e^{-j{2\pi \over \lambda f}(x_2 x_3 + y_2y_3)}dx_2 dy_2 \\ \propto \int \int^\infty_{-\infty} U_1({x_2 \over \lambda f}, {y_2 \over \lambda f}) e^{-j{2\pi \over \lambda f}(x_2 x_3 + y_2y_3)} d\xi \eta \\ \propto \mathcal{F} \{U_1({x_2 \over \lambda f}, {y_2 \over \lambda f})\}|_{\xi = {x_3 \over \lambda f}, \eta = {y_3 \over \lambda f}} \\ \propto u_1(-\lambda f\xi, -\lambda f \eta) = u_1(-x_3, -y_3)$$
위 결과는 ray tracing의 결과와 정확하게 일치한다. 즉, Magnification이 -1인 imag relay를 얻게 된다는 것이다. 실제로는 system의 exit pupil이 finitie size를 가져야 하지만, 우선은 Lens가 Infinite 한 size를 가지고, finite diffraction effects가 우리에게 아무런 문제를 일으키지 않는다고 가정하자.
1. Example : The diffraction grating
$(x_1, y_1)-$plane 상에 square-wave grating을 통과하는 plane wave가 있다고 가정할 때, 이것은 다음과 같은 field distribution을 가진다.
$$u_1(x_1, y_1) = rect({x\over 5\lambda}) * comb({x \over 10\lambda})$$
아래 그림은 위 field distribution을 나타낸 것이다. 실제로 field는 $x-$direction과 $y-$direction 모두에서 finite한 aperture를 가지지만, 당분간은 이를 무시하도록 하자.

Fourier Transform에 대한 지식을 통해 다음이 성립함을 알 수 있다.
$$u_1(x_1, y_1) = \sum^\infty_{n=-\infty} c_n e^{j{2\pi \over 10\lambda}x_1} \\ U_1(\xi, \eta) = \sum^\infty_{n=-\infty}c_n\delta(\xi - {n \over 10\lambda})\delta(\eta) \\ u_2(x_2) \propto \sum^\infty_{n=-\infty}c_n \delta({x_2\over \lambda f}-{n \over 10 \lambda})\delta({y_2 \over \lambda f}) \\ u_2(x_2) \propto \sum^\infty_{n=-\infty} c_n \delta(x_2 - {nf \over 10})\delta(y_2)$$
마지막 수식을 통해 알 수 있는 점은 Intermediate plane에서의 Field distribution이 $x_2 = {nf \over 10}$, $y_2 = 0$에서의 spot array이며, 연속적인 각 spot의 intensity는 $c_n^2$라는 점이다. 실제 system은 $\delta-$function에 의해 정의된 것처럼, Infinitely narrow spot을 가지고 있지 않지만, finite width(Airy disk와 같이)를 가지도록 modify 된다. 두 번째 Lens도 Fourier Transform을 하기 때문에 Output plane의 Intensity는 Input plane의 Intensity와 정확히 같을 것으로 예상된다.
Filtering
다음의 Transmission을 가지는 두 개의 Lens 사이의 Plane에 Transparency를 배치한다고 생각해보자.
$$T(x_2, y_2) = A_t(x_2, y_2) e^{-j\phi_t(x_2,y_2)}$$
Transparency가 존재하기 때문에 $(x_3, y_3)-$plane의 field는 다음과 같다.
$$u_3(x_3, y_3) \propto \mathcal{F} \{T(\xi, \eta)U_1(\xi, \eta)\}$$
Transparency는 original field distribution $u_1(x_1, y_1)$의 spaital frequency property를 modify 하는 spatial filter의 역할을 한다. Amplitude는 $A_t({x_2 \over \lambda f}, {y_2 \over \lambda f})$에 의해 주어진 amount 만큼 spatial frequency의 funciton으로 Attenuate(혹은 일반적으로 Amplify)되고 Phase는 $\phi_t({x_2 \over \lambda f}, {y_2 \over \lambda f})$에의해 주어진 amoutn 만큼 modify 된다.
1. Amplitude Filter
Binary Transparency는 Position에 따라 0 또는 1의 Transmission을 가지는 Transparency이다. 다음의 Transmission을 가지는 Slit의 effect에 대해 생각해 보자.
$$t(x_2, y_2) = rect({x_2 \over b})$$
이 Slit은 다음의 range에서 모든 Spatial Frequency를 허용한다.
$$-{b \over 2\lambda f} \leq \xi \leq {b \over 2\lambda f}$$
이 range를 벗어나는 모든 frequency는 completely attenuate 된다. Filter의 transmission은 아래 그림과 같으며, 이러한 유형의 filter를 Low-pass filter라고 한다.

이 경우 Slit은 가장 낮은 11개의 Diffraction order를 통과하게 한다. 아래 그림은 두 번째 Lens의 Back focal plane에서의 Intensity distribution을 보여준다. Slit이 High Frequency를 filtering 하였기 때문에 그 결과 Intensity는 완전한 square-wave가 아니게 된다.

2. Phase Filters
앞 Section에서는 Optical field의 Amplitude에만 영향을 미치는 Filter의 effect에 대해 설명하였다. 마찬가지로 우리는 Amplitude에는 영향을 주지 않고, Phase에만 영향을 미치는 Transparency를 만들 수 있다. 다음 그림과 같은 Transparency가 존재한다고 가정할 때, 이 Phase screen은 통과하는 모든 ray에 대해 ${a\lambda \over 2}$(a는 constant)와 동일한 amount의 OPL을 increase 한다.
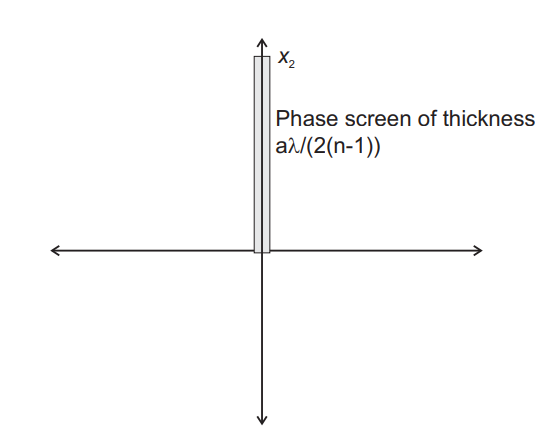
이는 다음의 수식에서 제시하는 Phase screen과 동일하다.
$$\phi(\xi) = a\pi step (x_2)$$
아래 그림은 $a$의 여러 값에 따른 Output plane의 intensity를 보여준다. phase filter는 Input Signal의 shape를 크게 distort 하는 effect를 가지고 있다.

2.1. Phase Filters
Linear Phase Filter는 special class phase filter 중 하나이며, Frequency domain에서 단순히 Complex sinusoid를 Transfer function으로 가지는 phase-only filter으로 다음과 같이 정의된다.
$$H(\xi) = e^{-j2\pi x_0 \xi}$$
이 Filter의 Phase는 $\xi$의 Linear function인 $\phi_H(\xi) = 2\pi x_0 \xi$이다. Input $f(x) \leftrightarrow F(\xi)$에 대한 이 filter의 output은 다음과 같다.
$$g(x) = \mathcal{F}^{-1} \{F(\xi) e^{-j2\pi x_0 \xi}\} \\ = f(x-x_0)$$
이를 통해 Linear phase filter가 output에서 offset을 생성한다는 것이 명백함을 알 수 있다.
2.2 Weak phase filter
Phase Transfer function이 $|\phi_H| << 1$과 같이 작은 경우에 대해 생각해보자. 이 경우 우리는 Taylor Series expansion을 통해 transfer function을 다음과 같이 쓸 수 있다.
$$H(\xi) = e^{-j\phi_H(\xi)} \approx 1-j\phi_H(\xi)$$
이 경우 우리는 Transfer function을 superposition으로 다음과 같이 쓸 수 있다.
$$H(\xi) \approx \delta(\xi) - j\phi_H(x)$$
이때, $\phi_H(x) \leftrightarrow \phi_H(\xi)$이다. 다음과 같은 예를 생각해보자.
$$\phi_H(\xi) = d \sin(2\pi b \xi), |d| << 1$$
이 transfer function은 weak sinusodial phase screen에서 볼 수 있는 것이다. 예를 들어 flat surface에 machining process에서 발생한 wavelength보다 훨씬 작은 preiodic pattern이 있는 경우 이러한 pattern이 발생할 수 있다. 이 경우 우리는 다음과 같이 쓸 수 있다.
$$\phi_H(\xi) = -j {|d| \over 2} [\delta(x-b) - \delta(x+b)]$$
이때 Approximate transfer function는 아래와 같다.
$$h(x) \approx \delta(x) - {|d| \over b}[\delta(x-b) - \delta(x+b)]$$
3. Combination filter
모든 실제 filter는 Amplitude filter와 Phae filter의 조합이다. 아래 그림은 Filter가 없는 경우, 11개의 lowest order를 pass 하는 Amplitude filter, Amplitude와 $a=0.5$의 값을 가지는 phase filter로 구성된 Combination filter의 output intensity를 나타낸 것이다.

High, Low and Bandpass filters
Low-Pass Filter(LPF), High-Pass Filter(HPF), Band-Pass Filter(BPF)는 매우 중요한 Filter이다. 이름에서 알 수 있듯이 이러한 Filter는 특성에 따라 spatial freqeuncy를 통과시킨다. Diffraction grating의 예로 돌아가 보자.
앞서 정의한 $t(x_2, y_2) = rect({x_2 \over b})$의 transparency를 가지고, $-{b \over 2\lambda f} \leq \xi \leq {b \over 2\lambda f}$의 frequency를 통과시키는 filter는 cutoff frequency 이하의 spatial frequency를 통과시키기 때문에 Low-Pass Filter라고 한다. 우리는 이 Filter가 square-wave grating의 transmission pattern을 따르는 것을 확인하였지만, sharp edge와 flat top correct가 완전히 일치하지 않은 점을 확인할 수 있다. 이를 보완하기 위해 아래와 같은 filter를 정의한다.
$$t_{hp}(x_2, y_2) = 1 - rect({x_2 \over b})$$
이 filter는 $|\xi| > {b \over (2\lambda f)}$의 frequency가 System을 통과할 수 있게 한다. 이 filter는 High spatial Frequency만을 통과시키기 때문에 High-Pass Filter이다. HPF와 LPF의 Output intensity는 아래 그림을 통해 확인할 수 있다.

'Optics > 이론' 카테고리의 다른 글
| Lec 12. Sampling & Reconstruction (2) | 2021.08.14 |
|---|---|
| Lec 11. Signal Processing (0) | 2021.08.13 |
| Lec 9. Hankel Transform, Fourier Bessel Transform, and Radon Transform (2) | 2021.08.12 |
| Lec 8. Two Dimensional Functions, Convolution, and Fourier Transforms (0) | 2021.08.11 |
| Lec 7. Special Properties and Important Theorems Involving the Fourier Transform (0) | 2021.08.03 |