본 게시물은 University of Arizona의 Prof. J. Scott Tyo의 OPTI512R 강의를 보고 정리한 내용입니다.
전공자가 아닌 만큼 부정확한 정보가 포함되어 있을 수 있습니다.
부정확한 정보가 있다면 알려주시면 감사하겠습니다.
Casting The Fresnel Integral In Polar Coordinates
Circular aperture과 object에서 Fresnel diffraction을 보면, circle의 center에 대한 rotation symmetry에서 비롯된 몇 가지 property를 볼 수 있다. 이 Symmetry를 유지하기 위해, Source 및 observation point 또한 axis위에 있다고 가정하도록 하자. 우리는 아래 그림과 같은 Fresnel diffraction expression을 생각해보자.
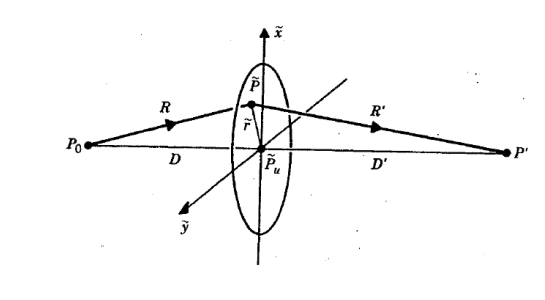
이때 Fresnel diffraction equation은 다음과 같다.
$$\begin{aligned}
u_{2}\left(x_{2}, y_{2}\right) &=\frac{e^{j k z_{12}}}{j \lambda z_{12}} \iint_{-\infty}^{\infty} u_{1}\left(x_{1}, y_{1}\right) \exp \left\{j \frac{\pi}{\lambda z_{12}}\left[\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}\right]\right\} d x_{1} d y_{1} \\
&=\frac{e^{j k z_{12}}}{j \lambda z_{12}} \iint_{-\infty}^{\infty} u_{1}\left(x_{1}, y_{1}\right) \exp \left\{j \frac{\pi}{\lambda z_{12}}\left[x_{1}^{2}+y_{1}^{2}\right]\right\} d x_{1} d y_{1} \\
&=\frac{e^{j k\left(z_{01}+z_{12}\right)}}{(j \lambda)^{2} z_{01} z_{12}} \iint_{-\infty}^{\infty} \tau\left(x_{1}, x_{2}\right) \exp \left\{j \frac{\pi}{\lambda z_{01}}\left[x_{1}^{2}+y_{1}^{2}\right]\right\} \exp \left\{j \frac{\pi}{\lambda z_{12}}\left[x_{1}^{2}+y_{1}^{2}\right]\right\} d x_{1} d y_{1} \\
&=\frac{e^{j k\left(z_{01}+z_{12}\right)}}{(j \lambda)^{2} z_{01} z_{12}} \iint_{-\infty}^{\infty} \tau\left(x_{1}, x_{2}\right) \exp \left\{j \frac{\pi}{\lambda}\left[\frac{1}{z_{01}}+\frac{1}{z_{12}}\right]\left[x_{1}{ }^{2}+y_{1}{ }^{2}\right]\right\} d x_{1} d y_{1}
\end{aligned}$$
우리는 paraxial approximation을 Aperture field $u_1(x_1, y_1)$에 대한 spherical wave으로 substituting 하고, axis에서 $x_2 = y_2 = 0$이라는 사실을 사용하여 이러한 simplification을 얻었다.
이 Equation을 cylindrical coordinates로 변환하는 것이 편리해 보인다. 또한 compactness를 위해 pre-factor를 drop 할 것이지만, coherent illumination을 사용하는 multiple aperture diffraction을 고려한다면, per-factor가 꽤나 중요한 역할을 한다는 것을 깨닫게 될 것이다.
$$\begin{aligned}
u_{2}\left(P^{\prime}\right) & \propto \int_{\rho_{1}=0}^{\infty} \int_{\phi_{1}=0}^{2 \pi} \tau\left(\rho_{1}, \phi_{1}\right) \exp \left\{j \frac{\pi}{\lambda \bar{z}} \rho_{1}^{2}\right\} \rho_{1} d \rho_{1} d \phi_{1} \\
&=2 \pi \int_{\rho_{1}=0}^{\infty} \tau\left(\rho_{1}, \phi_{1}\right) \exp \left\{j \frac{\pi}{\lambda \bar{z}} \rho_{1}^{2}\right\} \rho_{1} d \rho_{1}
\end{aligned}$$
위 수식에서 우리는 $\tau$가 azimuthally independent 하다고 가정했다. 또한 우리는 effective distance를 $\bar {z}^{-1} = z_{01}^{-1} = z_{12}^{-1}$으로 define 하였다. 만약 우리가 transmission function이 binary라고 가정하면(aperture inside에서 1, outside에서 0), 위 수식을 다음과 같이 정리할 수 있다.
$$\begin{aligned}
u_{2}\left(P^{\prime}\right) & \propto 2 \pi \int_{\tau} e^{j \frac{\pi}{\bar{x}} \rho_{1}{ }^{2}} \rho_{1} d \rho_{1} \\
& \propto \lambda \bar{z} \int_{\tau} e^{j u} d u
\end{aligned}$$
정리 과정에서 $u = (\pi, {\rho_1}^2)$로 variable을 변경하였다. 위 수식에서 u의 quantity는 $\rho_1$의 aperture에서 emerge 하는 wavefront part와 axis의 aperture를 exit 하는 wavefront part 사이의 phase difference이다. 위 수식에서 볼 수 있듯이, 이 phase variation은 quadratic 하고, azimuthally symmetric 하다.
Diffraction integral의 denominator에서, $r_{12}$의 factor를 $z_{12}$로 approximation 하였을 때, 우리는 $\psi =1$인 tacit paraxial approximation을 만들었다. Paraxial approximation에서 derivate 할 때, obliquity facotr는 위 수식의 inetgrand에 나타나야 한다. 여기서 우리는 이것을 $\cos\xi \approx 1$으로 가정했다.
만약 다음이 성립한다고 하면,
$$\tau(\rho_1) = cly({\rho_1 \over a})$$
integral은 다음과 같다.
$$\begin{aligned}
u_{2}\left(P^{\prime}\right) &\left.\propto \frac{\lambda}{j} e^{j u}\right|_{0} ^{\left(\pi a^{2}\right) /(4 \lambda \bar{z})} \\
&=\frac{\lambda \bar{z}}{j}\left[e^{j \frac{\pi a^{2}}{4 \lambda \bar{z}}}-1\right] .
\end{aligned}$$
이 integral의 결과는 아래 그림에 나타난 것과 같다. 우리는 $u$가 $2\pi$만큼 증가할 때마다, axis의 field에서 $0$을 얻는다. integrla의 net effect는 constructively interfere와 destructivley interfere를 반복하며 궁극적으로 아무것도 남기지 않는 것이다.
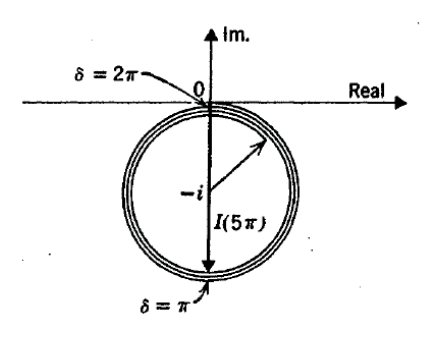
Fresnel Zones
geometrical optics와 physical optics 모두에서 lens가 aperture의 다른 부분을 통과하는 light의 phase를 변화시켜, 모든 light가 focus point에 constructively 하게 추가된다. 이 Lecture에서는 light가 phase로 add up 되는 aperture 부분만 통과하도록 함으로써, operate 하는 다른 유형의 "focusing" element에 대해 알아보도록 하겠다.
$$\begin{aligned}
u_{2}\left(P^{\prime}\right) & \propto 2 \pi \int_{\tau} e^{j \frac{\pi}{\bar{x}} \rho_{1}{ }^{2}} \rho_{1} d \rho_{1} \\
& \propto \lambda \bar{z} \int_{\tau} e^{j u} d u
\end{aligned}$$
앞서 정리한 위의 수식의 aperture가 Fresnel zone으로 divide 되는 것으로 생각하는 것이 좋다. Fresnel zone은 phase difference $u$가 각 zone에 걸쳐 $\pi$만큼 변경되고 n 번째 zone의 edge에서 $u = n\pi$만큼 변경되도록 define 된다. 물론 $\pi$의 phase change는 $\lambda/2$의 path length difference와 동일하다. source point가 $\infty$에 있는 경우에 대한 이 computation의 예시가 아래 그림에 나타나 있다.

n 번째 zone의 edge가 다음 위치에 있음을 쉽게 알 수 있다.
$$\rho_n = \sqrt{n\lambda z_{12}}$$
이 경우, $n^{th}$ zone의 area는 다음과 같고, $A_n$은 paraxial approximation에서 n과 independent하다.
$$A_n = \pi(n+1)\lambda z_{12} - \pi n\lambda z_{12} = \pi \lambda z_{12}$$
Obeservation point가 axis를 벗어나게 되면, source에서 observer로 직접 이동하는 shortest ray가 aperture의 center를 지나지 못하게 된다. 이 경우 Fresnel zone picture의 center는 반드시 아래 그림과 같이 Point $\tilde{P_{u}}$으로 adjust 해야 한다.
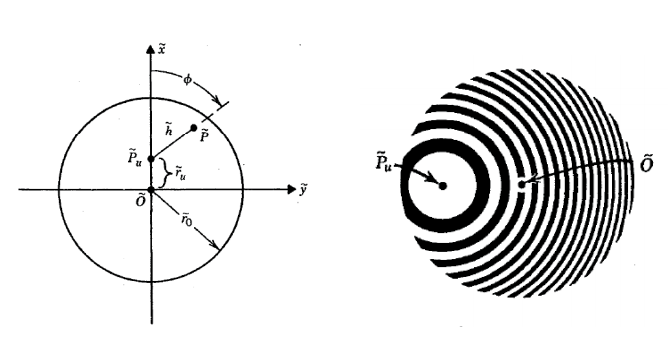
problem setting은 동일하지만, 이제 integral에는 asymmetric limit가 존재한다. 일부 zone의 경우, $\phi_1$ integral은 $0$에서 $2\pi$까지 이지만, 다른 zone들은 그렇지 않다.
Fresnel Zone Plates
만약 우리가 $0 \leq u \leq \pi$에서 field가 pass 할 수 있는 aperture를 construct 한다면, 이 aperture는 $\pi \leq u \leq 2\pi$에서는 field를 block 하고, $2\pi \leq u \leq 3\pi$에서는 다시 field를 pass 시키는 등, $\pi$마다 field의 pass와 block이 반복된다. 아래 그림과 같은 plate가 있을 때,

위 그림과 같은 plate를 aperture에 넣으면 아래 왼쪽 그림과 같던 phasor diagram이 아래 오른쪽 그림의 왼쪽과 같이 수정된다.
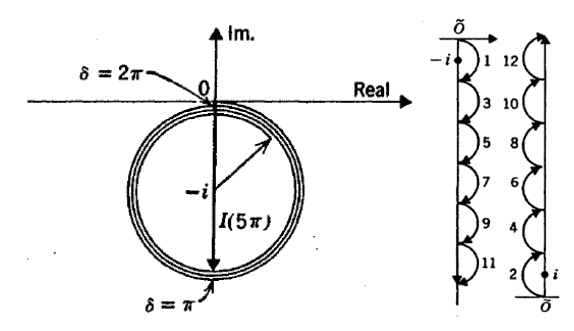
우리는(Imaginary part에 대해) destructively 하게 추가되는 integrand의 부분을 제거하고, integrand와 constructive 하게 add 되는 부분만을 유지하여, 우리가 관심 있는 지점에 집중할 수 있도록 해왔다. 이 방법은 다른 point에서 coherent addition을 produce하지 않을 것이고, 이를 제공하는 aperture device는 Fresnel zone plate로 알려져 있다.
'Optics > 이론' 카테고리의 다른 글
| Lec 20. Physical Optics Description of Imaging System (0) | 2021.08.27 |
|---|---|
| Lec 19. Fourier Transforming Properties of Lenses and Gaussian Cavities (1) | 2021.08.26 |
| Lec 17. Fresnel Diffraction (1) | 2021.08.24 |
| Lec 16. Fraunhofer Diffraction (0) | 2021.08.23 |
| Lec 15. Plane wave spectrum and Beams (0) | 2021.08.18 |