본 게시물은 University of Arizona의 Prof. J. Scott Tyo의 OPTI512R 강의를 보고 정리한 내용입니다.
전공자가 아닌 만큼 부정확한 정보가 포함되어 있을 수 있습니다.
부정확한 정보가 있다면 알려주시면 감사하겠습니다.
The Effect of Lenses on Propagating Fields
지금까지 우리는 Huygen's principle에 따라 field의 diffraction을 고려해왔다. 각 plane의 field를 spherical wave의 superposition으로 decompose 한 다음, spherical wave가 expand 하도록 함으로 써, field를 propagation 할 수 있다. 그런 다음, optical path에 lens를 도입하면 어떻게 되는지에 대해 고려한다. lens에 treatment는 Goodman의 treatment를 따를 것이다. Lens의 모든 point에서 우리는 lens의 thickness를 고려하고, lens가 해당 point를 pass 하는 field에 phase delay를 가져온다고 간주한다.

위 그림에서와 같이 single thin lens를 생각해보자. geometric optics에서와 같이 우리는 $(x,y)$ position에서, thin lens로 들어가는 wavefront는 동일한 position인 $(x,y)$로 나간다고 가정한다. lens의 thickness를 traversing 할 때, wavefront에 total phase delay가 발생한다.
$$\phi(x,y) = kn\triangle(x,y)+ k[\triangle_0 - \triangle(x,y)]$$
첫 번째 term은 lens material 내부에 accumulate 된 phase을 나타내고, 두 번째 term은 plane 사이의 propagation에서의 air distance를 나타낸다. 이 model에서 우리는 lens를 transmission function이 있는 pahse screen으로 간주할 수 있다.
$$t_{\ell}(x,y) = e^{jk \triangle_0}e^{jk(n-1)\triangle(x,y)}$$
Lens 바로 뒤의 field는 다음과 같이 쓸 수 있다.
$$u_\ell(x,y) = u_i(x,y) t_\ell(x,y)$$
The Lens Thickness Function
우리는 sign에 대한 standard optical conventions을 사용하여, lens의 thickness를 고려할 것이다. Curvature의 radius는 Curvature의 center가 vertex의 right에 있으면 positive로, Curvature center가 vertex의 left에 있으면 Negative로 간주된다.

위의 그림을 참조하여, 우리는 우리의 computation을 break 하여 thickness function을 build up 할 것이다. 우리는 우선 thickness $\triangle_{01}$과 $\triangle_{02}$로 시작할 것이다. 이러한 Thickness는 각각 positive혹은 negative일 수 있으며, thin lens의 center에서 lens의 vertex까지의 distance를 measure 한 값이 된다. 이러한 thickness는 임의의 position $(x,y)$에서 two piece로 split 할 수 있고, 이는 다음과 같다.
$$\begin{aligned}
\Delta_{1}(x, y) &=\Delta_{01}-\left(R_{1}-\sqrt{R_{1}^{2}-\left(x^{2}+y^{2}\right)}\right) \\
&=\Delta_{01}-R_{1}\left(1-\sqrt{\left.1-\frac{x^{2}+y^{2}}{R_{1}^{2}}\right)}\right.
\end{aligned}$$
위 그림의 Second surface의 경우, Curvature radius이 negative 하기 때문에, circle의 radius(positive 이어야 함)은 $-R_2$이고, thickness function은 다음과 같다.
$$\sqrt{1 - {{x^2+y^2} \over {R_1}^2}} \approx 1 -{1\over 2}{{x^2 + y^2}\over {R_1}^2}$$
$R_2$또한 위와 같다. $\triangle_{1}(x,y)$와 $\triangle_{2}(x,y)$에 이 approximation을 plugging 하면, 다음을 얻을 수 있다.
$$\begin{aligned}
\Delta_{1}(x, y) &=\Delta_{01}-\frac{x^{2}+y^{2}}{2 R_{1}} \\
\Delta_{2}(x, y) &=\Delta_{02}+\frac{x^{2}+y^{2}}{2 R_{2}} \\
\Delta(x, y) &=\Delta_{0}-\frac{x^{2}+y^{2}}{2}\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right) .
\end{aligned}$$
이 relationship을 통해 우리는 lens transmission function을 다음과 같이 정리할 수 있다.
$$t_{\ell}(x, y)=e^{j k n \Delta_{0}} \exp \left\{-j k(n-1) \frac{x^{2}+y^{2}}{2}\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\right\}$$
그리고 우리는 focal length를 다음과 같이 정의한다.
$${1 \over f} = (n-1) \bigg( {1\over R_1} - {1 \over R_2}\bigg)$$
위 수식은 Geometrical optics에서 얻은 focal length에 대한 definition과 정확하게 일치한다. 이제 우리는 lens transmission function을 다음과 같이 쓸 수 있다.
$$t_\ell(x,y) = e^{jkn \triangle_0 e^{-j{\pi \over \lambda f}(x^2 + y^2)}}$$
sign convention으로 thickness function을 구성하면 아래 그림과 같이 모든 shape의 lens를 처리할 수 있다.

Effect of Lenses on Optical Fields
Lens가 optical field를 어떻게 modify 하는지에 대한 diffraction perspective을 고려해보자. generality의 loss 없이, lens의 focal legth가 $f>0$이라고 가정한다. illuminating field가 아래의 expression을 이용하여, $+z$ direction으로 propagating 되는 spherical wave라고 가정하자.
$$u_i(x,y) = {e^{jkz} \over j\lambda z} e^{j {\pi \over {\lambda R_i}}(x^2 + y^2)}$$
만약 $R_i > 0$이면, 이는 curvature $R_i$의 radius를 가지는 diverging wave이다. 마찬가지로 $R_i < 0$이면, wave는 curvature radisu가 $-R_i$인 Converging wave이다. 만약 $R_i = \infty$이면, incident wave는 plane wave이다. Lens를 떠나는 Field는 다음과 같이 주어진다.
$$\begin{aligned}
u_{\ell}^{\prime}(x, y) &=u_{i}(x, y) t_{\ell}(x, y) \\
&=\frac{e^{j k z}}{j \lambda z} \exp \left\{j \frac{\pi}{\lambda}\left(\frac{1}{R_{i}}-\frac{1}{f}\right)\left(x^{2}+y^{2}\right)\right\}
\end{aligned}$$
우리는 이것을 아래와 같은 Curvature radius를 가지는 second spherical wave로 인식한다.
$${1\over R'} = {1\over R_i} - {1\over f}$$
따라서 paraxial approximation에서 lens는 incident spherical wave를 curvature radius가 다른 second shperical wave로 convert 하는 device이다. $R_i = f$일 때, 아래 그림과 같은 경우를 볼 수 있다. 마찬가지로, $0 < f < R_i$일 때, diverging spherical wave가 converging spherical wave로 convert 되고, $R_i < f <0$일 때, converging spherical wave가 diverging wave로 convert 된다.
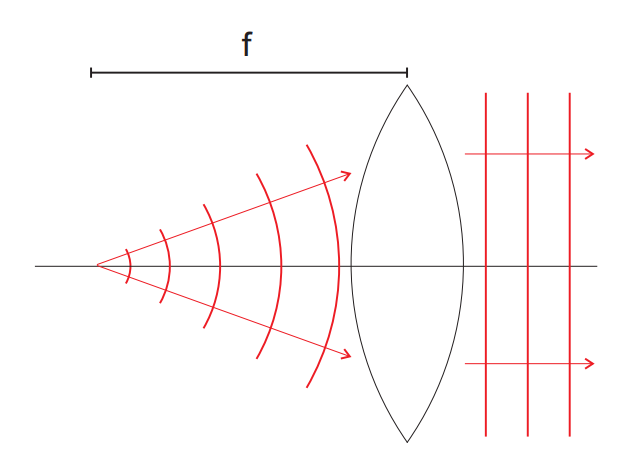
$R_i = 2f$인 경우 $R' = 2f$ 또한 성립하기 때문에, geometrical optic의 knowledge에 부합한다. 마지막으로, $R_i = \infty$일 때, lens에 plane wave가 incident 한다. output wave는 spherical wave이고, curvature radius는 $-f$이다. 만약 lens가 positive이면, output wave가 focal plane을 향해 converging 하는 것이고, Lens가 negative이면, output wave가 focal plane에서 멀어지는 것이다.
Object in Contact with The Lens
아래 그림에서와 같이 monochromatic, normally-incident, plane wvae illumination을 가진 lens에 obejct를 배치한다고 가정하자.

이때, Objec는 일반적으로 complex 한 transmission function $t_o(x,y)$를 가진다. 우리는 또한 lens가 $P(x,y)$에 의해 주어지는 finite 한 aperture를 가진다고 가정한다. Incident plane wave가 unit amplitude를 가진다고 가정할 때, 우리는 lens 바로 뒤에 있는 field를 다음과 같이 쓸 수 있다.
$$u'_{\ell}(x,y) = P(x,y) t_o(x,y) exp \bigg\{ -j {\pi \over \lambda f}(x^2 + y^2)\bigg\} $$
우리는 이제 diffraction을 사용하여 lens의 back focal plane field를 계산할 것이다. 우리는 lens 직후의 field를 알기 때문에, Fresnel diffraction formula를 사용하여 lens 뒤의 Fresnel zone에 있는 field를 계산할 수 있고, 이는 다음과 같다.
$$\begin{aligned}
u_{f}\left(x_{f}, y_{f}\right) &=\frac{e^{j k f} e^{j \frac{\pi}{\lambda f}\left(x_{f}^{2}+y_{f}^{2}\right)}}{j \lambda f} \mathcal{F}\left\{u_{\ell}^{\prime}(x, y) \exp \left\{j \frac{\pi}{\lambda f}\left(x^{2}+y^{2}\right)\right\}\right\} \\
&=\frac{e^{j k f} e^{j \frac{\pi}{\lambda f}\left(x_{f}^{2}+y_{f}{ }^{2}\right)}}{j \lambda f} \mathcal{F}\left\{P(x, y) t_{o}(x, y) \exp \left\{-j \frac{\pi}{\lambda f}\left(x^{2}+y^{2}\right)\right\} \exp \left\{j \frac{\pi}{\lambda f}\left(x^{2}+y^{2}\right)\right\}\right\} \\
&=\left.\frac{e^{j k f} e^{j \frac{\pi}{\lambda f}\left(x_{f}^{2}+y_{y}{ }^{2}\right)}}{j \lambda f} \mathcal{F}\left\{P(x, y) t_{o}(x, y)\right\}\right|_{\xi=\frac{x_{f}}{\lambda J}, \eta=\frac{y_{f}}{\lambda J}} \\
&=\left.\frac{e^{j k f} e^{j \frac{\pi}{\lambda J}\left(x_{f}^{2}+y_{y}{ }^{2}\right)}}{j \lambda f} \mathcal{F}\left\{P(x, y) U_{\ell}(x, y)\right\}\right|_{\xi=\frac{x_{f}}{\lambda f}, \eta=\frac{y_{f}}{\lambda f}}
\end{aligned}$$
우리는 위 수식을 통해 Back focal plane의 field가 object의 Fourier Transform에 proportional(Lense의 pupil function의 times) 하다는 것을 알 수 있다. 하지만 이것은 spherical wave curvature term을 가지고 있기 때문에, 정확한 Fourier Transform relationship이 아니다. 하지만 intensity에 대해서만 신경을 쓴다면 우리는 다음을 얻게 된다.
$$I(x_f, y_f) = |u_f(x_f, y_f)|^2 = {1 \over \lambda^2f^2}|\mathcal{F} \{P(x,y)t_o(x,y)\}|^2$$
Object in front of the Lens
다음으로, 우리는 아래 그림에서와 같이 lens로부터 $d_0$의 distance 만큼 떨어져 있는 obejct를 제거할 것이다. 우리는 Fresnel diffraction을 다음과 같이 쓸 수 있다.
$$u_\ell(x, y) = u_o(x, y) ∗ h_{12}(x, y)$$
또한 Impulse response를 다음과 같이 define 하였다.
$$h_{12}(x,y) = {e^{jkd_0} \over j\lambda d_0} exp \bigg \{ jk {\pi \over \lambda d_0}(x^2 + y^2)\bigg \}$$
Transfer function은 다음과 같다.
$$H_{12} (\xi, \eta) = e^{jkd_0} e^{-j\pi \lambda d_0(\xi^2 + \eta^2)}$$
이 정보들을 통해 우리는 다음을 쓸 수 있다.
$$U_\ell(ξ,η) = U_o(ξ,η)H_{12}(ξ,η)\\ u_\ell(x, y) = \mathcal{F}^{−1} \{U_o(ξ,η)H_{12}(ξ,η)\}$$
앞서 정의한 $u_f(x_f, y_f)$인 back focal plane의 field가 다음과 같이 주어진다는 것을 알고 있다.
$$\begin{aligned}
u_{f}\left(x_{f}, y_{f}\right) &=\left.\frac{e^{j k f} e^{j \frac{\pi}{\lambda f}\left(x_{f}^{2}+y_{y}^{2}\right)}}{j \lambda f} \mathcal{F}\left\{u_{\ell}(x, y)\right\}\right|_{\xi=\frac{x_{f}}{\lambda f}, \eta=\frac{y_{f}}{\lambda f}} \\
&=\frac{e^{j k f} e^{j \frac{\pi}{\lambda f}\left(x_{f}^{2}+y_{y}^{2}\right)}}{j \lambda f} e^{j k d_{o}} e^{-j \pi \frac{d_{o}}{\lambda f^{2}}\left(x_{f}{ }^{2}+y_{f}{ }^{2}\right)} U_{o}\left(\frac{x_{f}}{\lambda f}, \frac{y_{f}}{\lambda f}\right) \\
&=\frac{e^{j k\left(f+d_{o}\right)}}{j \lambda f} e^{j \frac{\pi}{\lambda f}\left(1-d_{o} / f\right)\left(x_{f}{ }^{2}+y_{f}{ }^{2}\right)} U_{o}\left(\frac{x_{f}}{\lambda f}, \frac{y_{f}}{\lambda f}\right)
\end{aligned}$$
위 수식은 $d_0 = f$인 특수한 경우 phase curvature를 완전히 제거하고, 정확한 Fourier Transform relationship을 가진다는 것을 나타낸다.
Effect of the Finite Aperture
이제까지 위의 Relationship들을 develope 하면서 우리는 $P(x,y) = 1$, 즉 lens가 Infinite 하다고 가정했다. Lense가 finite 할 때의 system의 동작을 이해하기 위해 우리는 ray optics에 대한 knowledge로 돌아갈 것이다.
아래 그림을 생각해보자. 우리는 Geometric optics를 통해 주어진 position $(x_f, y_f)$에 focus 된 모든 ray가 lens에 들어오는 parrallel ray로 시작한다는 것을 알고 있다. focal plane에서 멀어질수록, ray는 더 oblique 해진다. object가 extend 되므로, oblique angle로 propagating 되는 ray bundle은 angle이 커짐에 따라 더 많은 ray가 clip 된다. 즉, $(x_f, y_f)$에서 Fourier Transform의 intensity는 clipping을 통한 power lost의 비율로 attenuate 된다. 우리는 이러한 effect를 geometrical optics에서 오는 vignetting으로 인식한다.

Gaussian Beams Interacting with Lenses
Gaussian Beam은 expresssion으로 다음과 같이 describe 된다.
$$u(x,y,z) = {{b_0}^2 \over {b_0}^2 + j\lambda z} e^{jkz}e^{-\pi {r^2 \over b(z)^2}}e^{j {\pi \over \lambda R(z)}}$$
이때, $b(z)$와 $R(z)$는 다음과 같다.
$$b(z) = b_0 \sqrt{1 + \bigg({\lambda z \over {b_0}^2}\bigg)^2} \\ R(z) = z \bigg[ 1 + \bigg({{b_0}^2 \over \lambda z} \bigg)^2\bigg]$$
이 wave field에는 $z$의 function으로 변화하는 width의 Gaussian amplitude가 있다. 모든 position $z$에서 local phase curvature는 quadratic이다. 우리는 이 quadratic phase curvature가 radius $R(z)$의 curvature를 가지는 Spherical wave에 해당한다는 것을 알고 있다, $R>0$이면, wave는 diverging 하고, $R<0$이면 wave는 converging 한다. wave propagation은 아래 그림에 sketch 되어있다.

1. Gaussian Beam at the Focal Plnae of a Lens
아래 그림에 나온 것과 같이 Gaussian Beam이 Lense의 front focal plnae에 locate 해있다고 가정해보자. Input이 beam의 Waist에 있기 때문에 다음이 성립한다.
$$u_0(x_0, y_0) = Ae^{-\pi {r^2 \over {b_0}^2}}$$

이 field distribution은 lens에서 1 focal length만큼 떨어진 거리이다. 우리는 lens의 back focal plane의 field가 lens의 front focal plane의 field의 term에서 다음과 같이 주어진다는 것을 알고 있다.
$$\begin{aligned}
u_f(x_f , y_f) = {e^{2jkf}\over j\lambda f} \mathcal{F} \{u_o(x_o, y_o)\}|_{\xi= {x_f\over \lambda f} ,η= {y_f \over \lambda f}}
\\ = {e^{2jkf} \over j\lambda f} {b_0}^2 e^{−\pi{ {b_0}^2 \over (\lambda f)^2} r^2}
\end{aligned}$$
만약 우리가 다음과 같이 Input 및 output gaussian beam이 동일한 Special case를 고려한다면,
$${{b_0}^2 \over (\lambda f)^2} = {b_0}^2 \\ b_0 = \sqrt{\lambda f}$$
이 particular Gaussian Beam은 Lens의 Eigenmode이다.
2. Cavities

위 그림에 나타난 경우를 생각해보자. 이 geometry에서 우리는 각각 $2f$로 separate 된 identical lens series를 가지고 있다. 이 sketch는 identical spherical mirror가 있는 symmetric cavity lens-analog이다. mirror의 wavefront effect는 lens의 effect와 identical 하며, 각각의 reflection은 lens에 의해 equivalent diagram으로 replace 될 수 있다. 각 lens의 eigenmode를 identify 하였기 때문에, $b_0 = \sqrt {\lambda f}$를 만족시키는 Gaussian beam을 input 하면, system을 통해 unchaged propagation이 이루어진다는 것을 알 수 있다. 그러면, Gaussian beam이 cavity mode를 represent하고, 이는 laser와 optical amplifier에서 광범위하게 사용되는 중요한 사실이다.
3. Lenses acting on Gaussian Beam
이제 lens가 Gaussian Beam에 미치는 effect에 대해 알아보도록 하자. 편의를 위하여 우리는 lens가 Beam의 diameter보다 훨씬 크다고 가정할 것이며, 이는 우리가 lens를 infinite 하게 다룰 수 있다는 것을 의미한다.
만약 우리의 lens가 $f$의 focal length를 가진다면, 우리는 lens의 transmission function을 다음과 같이 쓸 수 있다.
$$t_{lens} = e^{-j {\pi \over \lambda f}(x^2 + y^2)}$$

lens가 만약 위 그림과 같이 incident beam의 beam waist를 기준으로 position $z$에 있으면, lens의 바로 뒤는 다음과 같다.
$$u'(x,y) = A(z)e^{-\pi {r^2 \over b^2(z)}} e^{j {\pi r^2 \over \lambda}\big({1\over R(z)} - {1\over f}\big)}$$
lens에서 나오는 wave는 Gaussian amplitude와 spherical wavefront를 가지지만, 앞서 살펴본 아래의 조건이 성립하지 않는 것을 확인 할 수 있다.
$$b(z) = b_0 \sqrt{1 + \bigg({\lambda z \over {b_0}^2}\bigg)^2} \\ R(z) = z \bigg[ 1 + \bigg({{b_0}^2 \over \lambda z} \bigg)^2\bigg]$$
논증을 위해 ${1\over f} > {1\over {R(z)}}$이라고 하자. 이는 lens에 Incident 하는 diverging spherical wavefront가 lens를 exiting 하는 converging wavefront로 convert 됨을 의미한다. wavefront가 spherical 하고, amplitude가 Gaussian임에 따라, lens에서 나오는 Beam 또한 Gaussian이라고 가정할 수 있지만, Lens 이후의 amplitude distribution $b(z)$와 wavefront curvature $R(z)$를 해결해야 한다. 이를 해결하는 과정은 Fresnel diffraction formula의 analysis를 통해 얻을 수 있다.
우리는 input beam waist에서 lens까지의 distance를 $S$로 하고, lens에서 output beam waist까지의 distance를 $S'$으로 정한다. 또한 우리는 Beam의 rayleigh range를 다음과 같이 define 할 수 있다.
$$z_0 = {{b_0}^2 \over lambda}$$
이 information을 활용하여, 우리는 Gaussian beam에 대해 equivalent 한 lens formula를 derive 할 수 있다.
$${1 \over s + jz_0} + {1 \over S' - jz'_0} = {1\over f}$$
Output beam waist는 다음과 같다.
$$b'_0 = b_0{f \over z_0}$$
'Optics > 이론' 카테고리의 다른 글
| Lec 21. Coherence of Optical Fields (0) | 2021.08.30 |
|---|---|
| Lec 20. Physical Optics Description of Imaging System (0) | 2021.08.27 |
| Lec 18. Fresnel Diffraction from Circular Apertures (0) | 2021.08.26 |
| Lec 17. Fresnel Diffraction (1) | 2021.08.24 |
| Lec 16. Fraunhofer Diffraction (0) | 2021.08.23 |